Dispersive Material Property

From openEMS

Note: This page is under construction. If you have experience with openEMS, please consider to create an account and help improve this page.

General Usage

 CSX = AddLorentzMaterial(CSX, name, varargin)

with the following parameters:

CSX: The original CSX structure
name: name of the property
varargin: a list of variable arguments

To define the material properties use:

 CSX = SetMaterialProperty(CSX, name, varargin)

with the following parameters:

CSX: The original CSX structure
name: name of this property (same as above!)
varargin: a list of variable arguments to define the properties:

Conventional material parameters:

Epsilon: relative electric permittivity for 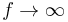$f \to \infty$ (must be >=1)
Mue: relative magnetic permeability for 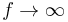$f \to \infty$ (must be >=1)
Kappa: electric conductivity (must be >=0)
Sigma: magnetic conductivity (non-physical property, must be >=0)

Drude material parameters:

EpsilonPlasmaFrequency: electric plasma frequency ( $f p l a s m a,1$ , see below)
MuePlasmaFrequency: magnetic plasma frequency
EpsilonRelaxTime: electric plasma relaxation time ( $τ p$ , losses, see below)
MueRelaxTime: magnetic plasma relaxation time (losses)

Drude higher order parameter (p>1):

EpsilonPlasmaFrequency_p: p-th order electric plasma frequency ( $f p l a s m a, p$ , see below)
MuePlasmaFrequency_p: p-th order magnetic plasma frequency
EpsilonRelaxTime_p: p-th order electric plasma relaxation time (losses)
MueRelaxTime_p: p-th order magnetic plasma relaxation time (losses)

Lorentz material parameters:

Note: Available only for openEMS >= v0.0.31!!

In addition to the drude parameter, the Lorentz-pole frequency can be defined:

EpsilonLorPoleFrequency: first electric Lorentz pole frequency ( $f L o r,1$ , see below)
EpsilonLorPoleFrequency_p: p-th electric Lorentz pole frequency ( $f L o r, p$ , see below)
MueLorPoleFrequency: first magnetic Lorentz pole frequency
MueLorPoleFrequency_p: p-th magnetic Lorentz pole frequency

Drude Material

Physical Model & Parameter

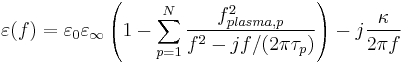
$\varepsilon(f) = \varepsilon_0\varepsilon_\infty \left( 1 - \sum_{p=1}^N \frac{f_{plasma,p}^2}{f^2-j f/(2\pi\tau_p)}\right) - j\frac{\kappa}{2\pi f}$

with the parameter:

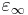$\varepsilon_\infty$ the relative permittivity for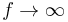 $f \to \infty$
$κ$ the electric conductivity
$f p l a s m a, p$ the p-th "plasma" frequency
$τ p$ the p-th relaxation time (damping)

Example

CSX = AddLorentzMaterial(CSX,'drude');
CSX = SetMaterialProperty(CSX,'drude','Epsilon',eps_r,'Kappa',kappa);
CSX = SetMaterialProperty(CSX,'drude','EpsilonPlasmaFrequency', 5e9, 'EpsilonRelaxTime', 5e-9);

Lorentz Material

Physical Model & Parameter

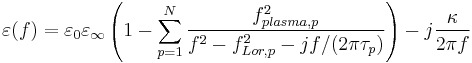
$\varepsilon(f) = \varepsilon_0\varepsilon_\infty \left( 1 - \sum_{p=1}^N \frac{f_{plasma,p}^2}{f^2-f_{Lor,p}^2-jf/(2\pi\tau_p)}\right) - j\frac{\kappa}{2\pi f}$

with the parameter:

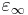$\varepsilon_\infty$ the relative permittivity for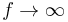 $f \to \infty$
$κ$ the electric conductivity
$f p l a s m a, p$ the p-th drude "plasma" frequency
$f L o r, p$ the p-th Lorentz pole frequency
$τ p$ the p-th relaxation time (damping)

Example

CSX = AddLorentzMaterial(CSX,'lorentz');
CSX = SetMaterialProperty(CSX,'lorentz','Epsilon',eps_r,'Kappa',kappa);
CSX = SetMaterialProperty(CSX,'lorentz','EpsilonPlasmaFrequency', 5e9, 'EpsilonLorPoleFrequency', 10e9, 'EpsilonRelaxTime', 5e-9);

Relation to other formulations

$\varepsilon(\omega) = \varepsilon_0\varepsilon_\infty + \varepsilon_0 \sum_{p=1}^N \frac{(\varepsilon_{dc,p}-\varepsilon_\infty)\omega^2_{p}}{\omega_{p}^2+2j\omega\delta_p-\omega^2}$

Conversion:

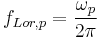
$f_{Lor,p} = \frac{\omega_{p}}{2\pi}$

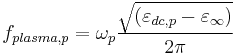
$f_{plasma,p} = \omega_{p}\frac{\sqrt{(\varepsilon_{dc,p}-\varepsilon_\infty)}}{2\pi}$

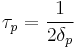
$\tau_p = \frac{1}{2\delta_p}$

$κ = 0$

Researchers in Physics often adopt a different sign convention, in which they use $e - i ω t$ for time-harmonic quantities rather than $e i ω t$ in engineering. Therefor in some textbook the Lorentz model is:

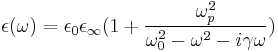
$\epsilon(\omega) = \epsilon_0\epsilon_{\infty} (1+ \frac{\omega_p^2}{\omega_0^2 - \omega^2 - i\gamma \omega})$

And the Drude model is:

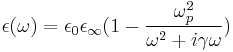
$\epsilon(\omega) = \epsilon_0\epsilon_{\infty} (1- \frac{\omega_p^2}{\omega^2 + i\gamma \omega})$

Where $ω p$ is the plasma frequency and $ω 0$ is the plasmonic resonant frequency and $γ$ represents the damping effect in material.

Dispersive Material Property

From openEMS

Contents

General Usage

Conventional material parameters:

Drude material parameters:

Drude higher order parameter (p>1):

Lorentz material parameters:

Drude Material

Physical Model & Parameter

Example

Lorentz Material

Physical Model & Parameter

Example

Relation to other formulations

Navigation

documentation