Tutorial: Bent Patch Antenna

From openEMS

Jump to: navigation, search

Download the latest matlab file using Github: Bent_Patch_Antenna.m

Bent patch antenna model

This tutorial covers

setup of a Bent Patch Antenna (see for comparison: Tutorial: Simple Patch Antenna)
setup of a cylindrical FDTD mesh
calculate the S-Parameter and input impedance
calculate far-field pattern 2D/3D

Matlab Simulation Script

Start the script within an empty environment:

close all
clear
clc

Specify drawing units

physical_constants;
unit = 1e-3; % all length in mm

Specify the patch size, substrate properties, and feed point

% patch width in alpha-direction
patch.width  = 32; % resonant length in alpha-direction
patch.radius = 50; % radius
patch.length = 40; % patch length in z-direction
 
%substrate setup
substrate.epsR   = 3.38;
substrate.kappa  = 1e-3 * 2*pi*2.45e9 * EPS0*substrate.epsR;
substrate.width  = 80;
substrate.length = 90;
substrate.thickness = 1.524;
substrate.cells = 4;
 
%setup feed point
feed.pos = -5.5;   %feeding position in x-direction
feed.width = 2;  %feeding port width
feed.R = 50;     %feed resistance

Set up the simulation

Note that the coordinate system is set to cylindrical.

% size of the simulation box
SimBox.rad    = 2*100;
SimBox.height = 1.5*200;
 
%% setup FDTD parameter & excitation function
FDTD = InitFDTD('CoordSystem', 1); % init a cylindrical FDTD
f0 = 2e9; % center frequency
fc = 1e9; % 20 dB corner frequency
FDTD = SetGaussExcite( FDTD, f0, fc );
BC = {'MUR' 'MUR' 'MUR' 'MUR' 'MUR' 'MUR'}; % boundary conditions
FDTD = SetBoundaryCond( FDTD, BC );
 
%% setup CSXCAD geometry & mesh
% init a cylindrical mesh
CSX = InitCSX('CoordSystem',1);

Calculate angular sizes

Calculate angular sizes (in radians) for the patch width, substrate width, and position of the feed point.

patch_ang_width = patch.width/(patch.radius+substrate.thickness);
substr_ang_width = substrate.width/patch.radius;
feed_angle = feed.pos/patch.radius;

Now create the objects

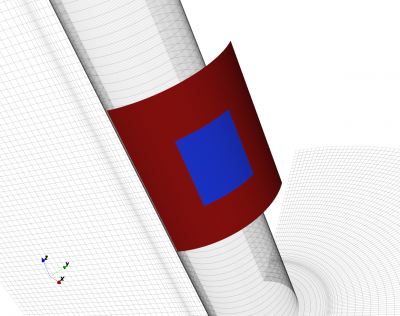
Note that although the patch and substrates are curved objects, the function AddBox is used. In a cylindrical coordinate system the start/stop coordinates are in the form [ radius azimuth z ].

%% create patch
CSX = AddMetal( CSX, 'patch' ); % create a perfect electric conductor (PEC)
start = [patch.radius+substrate.thickness -patch_ang_width/2 -patch.length/2 ];
stop  = [patch.radius+substrate.thickness  patch_ang_width/2  patch.length/2 ];
CSX = AddBox(CSX,'patch',10,start,stop); % add a box-primitive to the metal property 'patch'
 
%% create substrate
CSX = AddMaterial( CSX, 'substrate' );
CSX = SetMaterialProperty( CSX, 'substrate', 'Epsilon', substrate.epsR, 'Kappa', substrate.kappa );
start = [patch.radius                     -substr_ang_width/2 -substrate.length/2];
stop  = [patch.radius+substrate.thickness  substr_ang_width/2  substrate.length/2];
CSX = AddBox( CSX, 'substrate', 0, start, stop);

Add a dump box for the surface current on the patch

CSX = AddDump(CSX, 'Jt_patch','DumpType',3,'FileType',1);
start = [patch.radius+substrate.thickness -substr_ang_width/2 -substrate.length/2];
stop  = [patch.radius+substrate.thickness +substr_ang_width/2  substrate.length/2];
CSX = AddBox( CSX, 'Jt_patch', 0, start, stop );

A ground plane is placed on the backside of the substrate

Note that this metal structure has zero thickness.

CSX = AddMetal( CSX, 'gnd' ); % create a perfect electric conductor (PEC)
start = [patch.radius -substr_ang_width/2 -substrate.length/2];
stop  = [patch.radius +substr_ang_width/2 +substrate.length/2];
CSX = AddBox(CSX,'gnd',10,start,stop);

Add an excitation port

start = [patch.radius                      feed_angle 0];
stop  = [patch.radius+substrate.thickness  feed_angle 0];
[CSX port] = AddLumpedPort(CSX, 50 ,1 ,feed.R, start, stop, [1 0 0], true);

Define the mesh

The simulation space is a C-shaped extrusion which extends from -135° to +135° in azimuth.

Bent patch antenna mesh

% detect all edges
mesh = DetectEdges(CSX);
 
% add the simulation domain size
mesh.r = [mesh.r patch.radius+[-20 SimBox.rad]];
mesh.a = [mesh.a -0.75*pi 0.75*pi];
mesh.z = [mesh.z -SimBox.height/2 SimBox.height/2];
 
% add some lines for the substrate
mesh.r = [mesh.r patch.radius+linspace(0,substrate.thickness,substrate.cells)];
 
% generate a smooth mesh with max. cell size: lambda_min / 20
max_res = c0 / (f0+fc) / unit / 20;
max_ang = max_res/(SimBox.rad+patch.radius); % max_res in radians
mesh = SmoothMesh(mesh, [max_res max_ang max_res], 1.4);
 
disp(['Num of cells: ' num2str(numel(mesh.r)*numel(mesh.a)*numel(mesh.z))]);
CSX = DefineRectGrid( CSX, unit, mesh );

Create a NF2FF box

Again, even though this is called a box, because the coordinate system is set to cylindrical, the arguments will be assumed as [ radius azimuth z ].

%% create nf2ff, keep some distance to the boundary conditions, e.g. 8 cells pml
start = [mesh.r(4)     mesh.a(8)     mesh.z(8)];
stop  = [mesh.r(end-9) mesh.a(end-9) mesh.z(end-9)];
[CSX nf2ff] = CreateNF2FFBox(CSX, 'nf2ff', start, stop, 'Directions',[1 1 1 1 1 1]);

Save and run the simulation

%% prepare simulation folder & run
Sim_Path = ['tmp_' mfilename];
Sim_CSX  = [mfilename '.xml'];
 
[status, message, messageid] = rmdir( Sim_Path, 's' ); % clear previous directory
[status, message, messageid] = mkdir( Sim_Path ); % create empty simulation folder
 
% write openEMS compatible xml-file
WriteOpenEMS( [Sim_Path '/' Sim_CSX], FDTD, CSX );
 
% show the structure
CSXGeomPlot( [Sim_Path '/' Sim_CSX] );
 
% run openEMS
RunOpenEMS( Sim_Path, Sim_CSX);

Post Processing

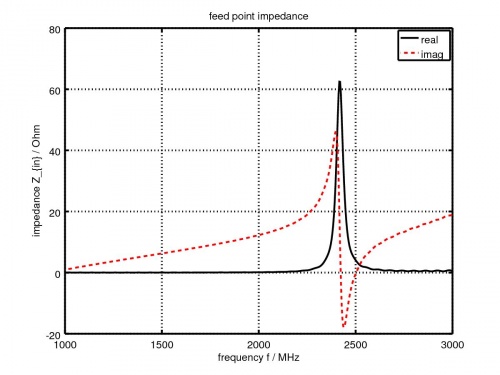
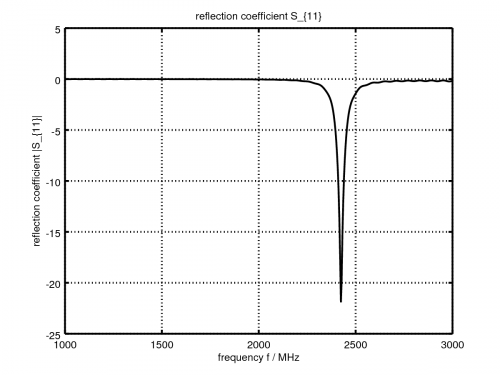
Plot the feed-point impedance and reflection coefficient

freq = linspace( max([1e9,f0-fc]), f0+fc, 501 );
port = calcPort(port, Sim_Path, freq);
 
Zin = port.uf.tot ./ port.if.tot;
s11 = port.uf.ref ./ port.uf.inc;
P_in = 0.5*real(port.uf.tot .* conj(port.if.tot)); % antenna feed power
 
% plot feed point impedance
figure
plot( freq/1e6, real(Zin), 'k-', 'Linewidth', 2 );
hold on
grid on
plot( freq/1e6, imag(Zin), 'r--', 'Linewidth', 2 );
title( 'feed point impedance' );
xlabel( 'frequency f / MHz' );
ylabel( 'impedance Z_{in} / Ohm' );
legend( 'real', 'imag' );
 
% plot reflection coefficient S11
figure
plot( freq/1e6, 20*log10(abs(s11)), 'k-', 'Linewidth', 2 );
grid on
title( 'reflection coefficient S_{11}' );
xlabel( 'frequency f / MHz' );
ylabel( 'reflection coefficient |S_{11}|' );
 
drawnow

Determine the resonant frequency and save the current distribution for plotting

This is done by finding the frequency index for the minimum value of s11, and then using the index to determine the frequency.

%find resonance frequency from s11
f_res_ind = find(s11==min(s11));
f_res = freq(f_res_ind);
 
%%
disp('dumping resonant current distribution to vtk file, use Paraview to visualize');
ConvertHDF5_VTK([Sim_Path '/Jt_patch.h5'],[Sim_Path '/Jf_patch'],'Frequency',f_res,'FieldName','J-Field');

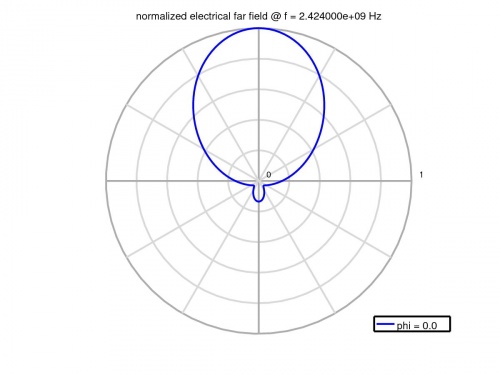
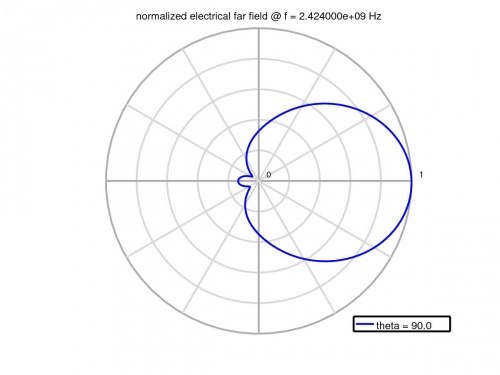
Calculate and plot the far-field patterns etc.

% calculate the far field at phi=0 degree
nf2ff = CalcNF2FF(nf2ff, Sim_Path, f_res, [-180:2:180]*pi/180, 0,'Center',[patch.radius+substrate.thickness 0 0]*unit, 'Outfile','pattern_phi_0.h5');
% normalized directivity as polar plot
figure
polarFF(nf2ff,'xaxis','theta','param',1,'normalize',1)
 
% calculate the far field at phi=0 degree
nf2ff = CalcNF2FF(nf2ff, Sim_Path, f_res, pi/2, (-180:2:180)*pi/180,'Center',[patch.radius+substrate.thickness 0 0]*unit, 'Outfile','pattern_theta_90.h5');
% normalized directivity as polar plot
figure
polarFF(nf2ff,'xaxis','phi','param',1,'normalize',1)
 
% display power and directivity
disp( ['radiated power: Prad = ' num2str(nf2ff.Prad) ' Watt']);
disp( ['directivity: Dmax = ' num2str(nf2ff.Dmax) ' (' num2str(10*log10(nf2ff.Dmax)) ' dBi)'] );
disp( ['efficiency: nu_rad = ' num2str(100*nf2ff.Prad./real(P_in(f_res_ind))) ' %']);
 
drawnow
 
%%
disp( 'calculating 3D far field pattern and dumping to vtk (use Paraview to visualize)...' );
thetaRange = (0:2:180);
phiRange = (0:2:360) - 180;
nf2ff = CalcNF2FF(nf2ff, Sim_Path, f_res, thetaRange*pi/180, phiRange*pi/180,'Verbose',1,'Outfile','3D_Pattern.h5','Center',[patch.radius+substrate.thickness 0 0]*unit);
 
figure
plotFF3D(nf2ff,'logscale',-20);